只针对有向无环图（DAG, Directed Acylic Graph），用于将图从“根”到“叶子”提溜出来。

拓扑排序解决的是节点之间的前后排序问题，对于拓扑排序的结果，如果i位于j前面，则只要i和j之间存在有向路径，那么i就一定是这条路径的起点。

经典的拓扑排序应用就是解决活动的前置依赖问题，用顶点表示活动，用弧表示活动之间的优先关系，求每个活动的前置依赖，或者给出每个活动的前置依赖，求能否完成所有的活动。

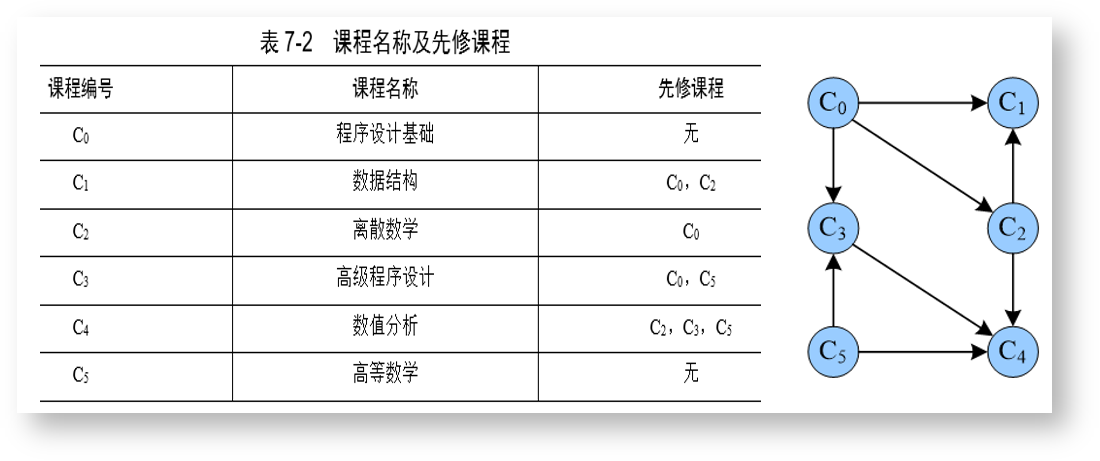
以选修课程为例，每个课程都可能有前置课程，只有学完前置的课程才能学习当前课程，给出所有的课程以及它们的前置课程，问能不能顺利学完这些课程，以及学习的顺序应该是怎么样的：

注意：拓扑排序的结果并不是唯一的。

拓扑排序还可以用于判断环，当图中存在环，说明存在互相依赖的前置关系，一定是无法对全部结点进行拓扑排序的。

算法设计：

1. 求出各顶点的入度，并将所有入席为0的顶点入栈。
2. 在栈不为空的情况下，重复执行以下操作：
   1. 栈顶元素出栈，并保存到拓扑排序结果数组topo[]中；
   2. 顶点元素的所有邻接点入度减1，如果减1后入度为0，则入栈。
3. 栈为空之后，如果拓扑排序输出的顶点数小于顶点总数，则说明有环，否则拓扑排序完成。

除了可以用栈来实现拓扑排序，还可以直接借助递归来实现，以下是拓扑排序的代码示例：