只针对有向无环图（DAG, Directed Acylic Graph），用于将图从“根”到“叶子”提溜出来。

拓扑排序解决的是节点之间的前后排序问题，对于拓扑排序的结果，如果i位于j前面，则只要i和j之间存在有向路径，那么i就一定是这条路径的起点。

经典的拓扑排序应用就是解决活动的前置依赖问题，用顶点表示活动，用弧表示活动之间的优先关系，求每个活动的前置依赖，或者给出每个活动的前置依赖，求能否完成所有的活动。

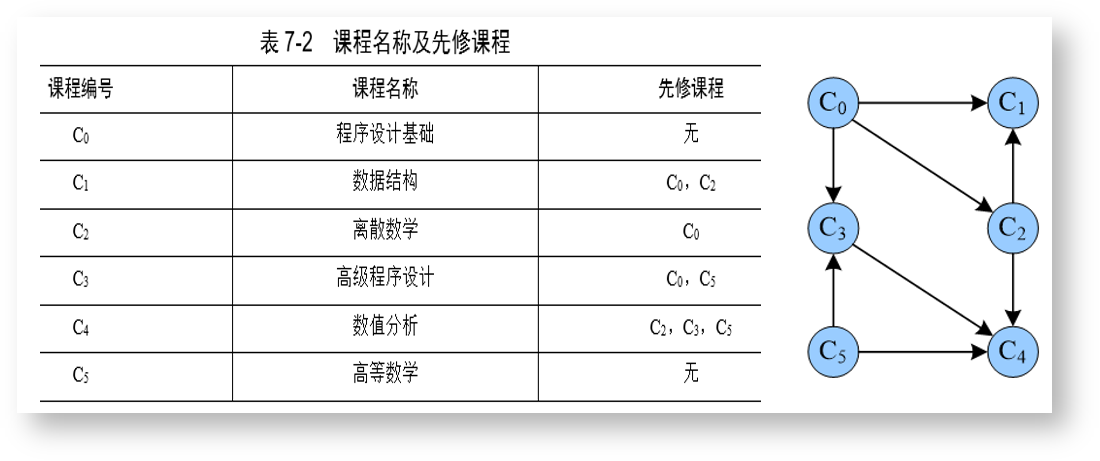
以选修课程为例，每个课程都可能有前置课程，只有学完前置的课程才能学习当前课程，给出所有的课程以及它们的前置课程，问能不能顺利学完这些课程，以及学习的顺序应该是怎么样的：

注意：拓扑排序的结果并不是唯一的。

拓扑排序还可以用于判断环，当图中存在环，说明存在互相依赖的前置关系，一定是无法对全部结点进行拓扑排序的。

算法设计：

  1. 求出各顶点的入度，并将所有入度为0的顶点入栈。
  2. 在栈不为空的情况下，重复执行以下操作：
    1. 栈顶元素出栈，并保存到拓扑排序结果数组topo[]中；
    2. 顶点元素的所有邻接点入度减1，如果减1后入度为0，则入栈。
  3. 栈为空之后，如果拓扑排序输出的顶点数小于顶点总数，则说明有环，否则拓扑排序完成。

除了可以用栈来实现拓扑排序，还可以使用队列，或者直接借助递归来实现，以下是拓扑排序的代码示例：

#define MAXN 1005

vector<int> G[MAXN]; // 邻接表，G[i]表示i指向的结点
int n;               // 结点数

int topsort() {
    // 计算各个顶点的入度
    vector<int> indegree(n);
    for(int i = 0; i < n; i++) {
        for(auto &t : G[i]) {
            indegree[t]++;
        }
    }

    // 入度为0的先入队
    queue<int> Q;
    for(int i = 0; i < n; i++) {
        if(indegree[i] == 0) {
            Q.push(i);
        }
    }

    // 拓扑排序
    int count = 0;
    while(!Q.empty()) {
        int cur = Q.front();
        Q.pop();
        count++;
        for(auto &t : G[cur]) { // 邻接点入度减1，如果为0，则入队
            indegree[t]--;
            if(indegree[t] == 0) {
                Q.push(t);
            }
        }
    }
    
    return count;
}

DFS+三色标记法形式：

#define MAXN 1005

vector<int> G[MAXN]; // 邻接表，G[i]表示i指向的结点
int n;               // 结点数

int visited[MAXN];   // 访问状态，0：未访问，1：访问中，2：已访问
int count;           // 结点计数
bool valid;          // 记录是否是合法的DAG，也就是是否存在环

void dfs(int u) {
    visited[u] = 1;
    for(auto &v : G[u]) {
        if(visited[v] == 0) {
            dfs(v);
        } else if(visited[v] == 1) {
            valid = false;
        }
    }
    visited[u] = 2;
    count++;
}

int topsort_DFS() {
    count = 0;
    valid = true;
    for(int i = 0; i < n; i++) {
        dfs(i);
    }
    return count;
}