最小生成树代表的问题是如何以最小的代价将所有结点连接起来，比如典型地求游历全部城市的最小旅行费用，求给村庄接通电线的最短布线。

具体来说，最小生成树是指从图里选出n-1条边，将所有n个结点连接起来构成一棵树（不能存在环），并且使所有边的权值最小。除最小生成树外，还有子图，生成子图，生成树等概念。

最小生成树不是唯一的，比如存在多条边权值相同时，最小生成树就可能不止一种。

一个结点发出的最小边一定是最小生成树里的一条边，但是只按这种算法并不能得到全部的最小生成树的边，因为有些边可能被两个结点共用了，导致不满足n-1条边。

由于最小生成树对应的图是n个结点n-1条边，也就是没有冗余，断一条边图就不连通了。

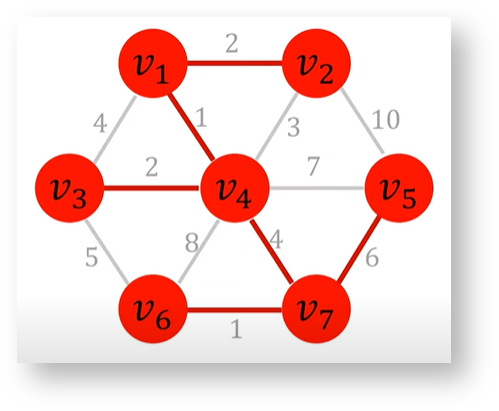
数据结构与算法 > 最小生成树 > image2022-3-30_11-19-20.png

Prim算法

把已经在生成树中的结点看作一个集合，剩下结点看作另一个集合，从连接两个集合的边中选择一条权值最小的边。

初始时可以任意选取一个点作为Prim算法的起点，为了记录最小生成树的生长过程和每个点的生成树权值，使用closest数组来记录结点j离当前生成数中最近的结点，使用lowcost数组来记录结点j离生成树中最近的结点的权值，另外还需要一个数组visited来记录哪些节点已经被访问。

Prim算法的代码如下：

#define MAXN 1005
#define INF 0x3f3f3f3f

int G[MAXN][MAXN]; // 邻接矩阵，G[u][v]表示顶点u到顶点v的距离，或者为INF，表示u、v之间不存在边
int n;             // 顶点数

int closest[MAXN]; // closest[i]表示结点i离当前生成树中最近的结点
int lowcost[MAXN]; // lowcost[i]表示结点i离当前生成树中最近的结点的权值，即(i, closest[i])
int visited[MAXN]; // 表示顶点i是否已访问过

int prim() {
    // 初始化
    for(int i = 0; i < n; i++) {
        lowcost[i] = G[0][i];
        closest[i] = 0;
        visited[i] = false;
    }

    visited[0] = true; // 从顶点0开始进行生成MST

    for(int i = 0; i < n; i++) {
        int tmp = INF, t = 0;
        for(int j = 0; j < n; j++) { // 在剩下点中寻找lowcost最小的节点t
            if(!visited[j] && lowcost[j] < tmp) {
                tmp = lowcost[j];
                t = j;
            }
        }
        if(t == 0) return 0; // 找不到，说明这是非连通图，不存在MST
        visited[t] = true;
        for(int j = 0; j < n; j++) { // 遍历与t相连的点，更新lowcost和closest
            if(G[t][j] != INF && !visited[j] && G[t][j] < lowcost[j]) {
                lowcost[j] = G[t][j];
                closest[j] = t;
            }
        }
    }

    int sumcost = 0;
    for(int i = 0; i < n; i++) {
        sumcost += lowcost[i];
    }
    return sumcost;
}

Kruskal算法

Kruskal算法使用了并查集的思想，初始时将n个顶点看成各自独立的连通分量，然后将所有边按权值从小到大排序，然后做贪心选择：

选取边集E中权值最小的边。
连接这条边的两个顶点，看是否产生环，即find(u) == find(v)，如果不产生环，则这条边就是最小生成树中的一条边，将边从边集E中删除，并合并两个顶点u和v：merge(u, v)。
以上操作重复n-1次，得到的就是全部最小生成树的边。

边集数组的存储形式与Kruskal算法比较契合，因为可以直接对边进行排序，并且输出的结果也是一个边集数组。

示例代码：

#define MAXN 1005
#define INF 0x3f3f3f3f

// 并查集
class DSU {
public:
    DSU(int n) {...}
    int find(int x) {...}
    void merge(int x, int y) {...}
};

struct Edge {
    int u; // 起点
    int v; // 终点
    int w; // 权值
    bool operator<(const Edge &other) {
        return w < other.w;
    }
}; 

Edge G[MAXN];   // 边集数组
int n;          // 顶点数
int m;          // 边数

int kruskal() {
    DSU dsu(n); // 定义并查集
    sort(G, G + m); // 所有边从小到大排序

    int ans = 0; // 记录MST的权值
    int cnt = 0; // 记录当前已经使用的条的数目
    for(int i = 0; i < m; i++) {
        int u = G[i].u;
        int v = G[i].v;
        int w = G[i].w;
        if(dsu.find(u) == dsu.find(v)) continue; // 这条边无助于生成MST
        dsu.merge(u, v);    // 合并两条个顶点
        ans += w;           // 更新权值
        cnt++;              // 更新已使用的边的数目
							// 还可以把使用过的边保存起来，以得到最后的MST
        if(cnt == n-1) {    // 边的数目达到顶点数减1时，表示MST已构建完成
            break;
        }
    }
    return ans;
}