哈夫曼编码

变长编码，常用于压缩，可使编码总长度最短。

哈夫曼编码是一种前缀码，通过唯一前缀来区分二义性。

总得来说，如果给出了一些待编码的项和它们的出现频率，就可以通过哈夫曼编码来给每个项设置一个编码值，这个编码值可以保证是唯一的，且编码后的总长度最短，也就是sum{每个项的长度 * 出现频率}值最小。以下是一个示例，针对字符进行哈夫曼编码：

字符	a	b	c	d	e	f
频率	0.05	0.32	0.18	0.07	0.25	0.13

编码后的结果：

字符	a	b	c	d	e	f
频率	1000	11	00	1001	01	101

假设一篇文档只包括这几个字符，那么以上面的编码来进行保存，可以保证得到的文档大小一定是最小的，而且能够无歧义地通过唯一前缀来解析出文档的内容。

哈夫曼编码将所有的待编码字符作为叶子节点，将该字符的频率作为叶子节点的权值，以自底向上的方式，通过n-1次“合并”构造哈夫曼树。

哈夫曼编码的核心思想：权值大的离根近。

哈夫曼编码的贪心策略：每次从树的集合中取出没有双亲且权值最小的两棵树作为左右子树，构造一棵新树，新树根节点的权值为其左右孩子节点权值之和，并将新树插入树的集合中。

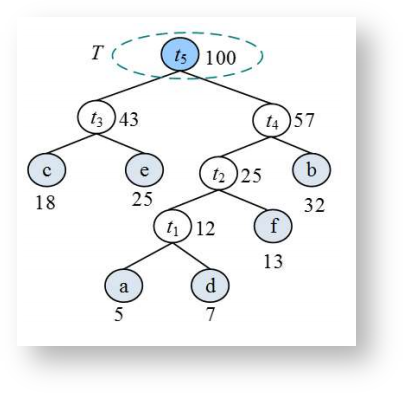
约定左分支上的编码为"0"，右分支上的编码为"1"，从根结点到叶子节点路径上的字符组成的字符串就是该叶子节点的哈夫曼编码。以下为上面表格中字符的哈夫曼编码树（权值放大了100倍，方便处理）：

哈夫曼树中只有度为0的叶子结点和度为2的非叶子结点，它们的数量关系是n0 = n2 + 1。

示例代码：

#define MAXBIT 100 // 哈夫曼编码的最大长度
#define MAXLEAF 30 // 最多可以对30个结点进行哈夫曼编码
#define MAXNODE (MAXLEAF*2 - 1) // 哈夫曼树的最大结点数，公式 n0 = n2 + 1

typedef struct //节点结构体
{
    char value;    //结点内容
    double weight; //结点权值
    int parent;    //双亲
    int lchild;    //左孩子
    int rchild;    //右孩子
} HNodeType;

typedef struct //编码结构体
{
    int bit[MAXBIT];
    int start; // start+1位开始存储哈夫曼编码
} HCodeType;

HNodeType HuffNode[MAXNODE]; //定义一个节点结构体数组
HCodeType HuffCode[MAXLEAF]; //定义一个编码结构体数组
int n; // 叶子结点数

struct Node {
    double weight; // 权值
    int index;     // 编号
    Node() {}
    Node(double w, int i) : weight(w), index(i) {}
    bool operator<(const Node &other) const {
        return weight > other.weight;
    }
};

// 构造哈夫曼树
void HuffmanTree() {
    // 初始化哈夫曼树全部的结点
    for(int i = 0; i < 2 * n - 1; i++) {
        HuffNode[i].weight = 0;
        HuffNode[i].parent = -1;
        HuffNode[i].lchild = -1;
        HuffNode[i].rchild = -1;
    }

    // 输入n个叶子的信息
    cout << "Please input value and weight of leaf node :" << endl;
    for(int i = 0; i < n; i++) {
        cin >> HuffNode[i].value >> HuffNode[i].weight;
    }

    // 定义优先队列并将所有结点入队
    priority_queue<Node> Q;
    for(int i = 0; i < n; i++) {
        Q.push({HuffNode[i].weight, i});
    }

    // 执行n-1次合并，生成哈夫曼树
    for(int i = 0; i < n-1; i++) {
        // 选出当前权值最小的两个结点
        Node n1, n2;
        n1 = Q.top();
        Q.pop();
        n2 = Q.top();
        Q.pop();
        // 开辟一个新结点作为这两个结点的父结点
        // 父结点权值为两个结点的权值之和
        // 父结点具有左右孩子结点
        HuffNode[n1.index].parent = n + i;
        HuffNode[n2.index].parent = n + i;
        HuffNode[n + i].weight = n1.weight + n2.weight;
        HuffNode[n + i].lchild = n1.index;
        HuffNode[n + i].rchild = n2.index;
        // 父结点也入队
        Q.push({HuffNode[n + i].weight, n + i});
    }
}

// 计算每个叶子结点的哈夫曼编码
void HuffmanCode() {
    HCodeType tmp;
    int cur, parent;
    for(int i = 0; i < n; i++) {
        tmp.start = n-1; // 从最后一位开始往前存储哈夫曼编码
        cur = i;
        parent = HuffNode[cur].parent;
        while(parent != -1) { // 从叶子结点开始往上寻找父结点并计算当前的编码值
            if(HuffNode[parent].lchild == cur) {
                tmp.bit[tmp.start] = 0;
            } else {
                tmp.bit[tmp.start] = 1;
            }
            tmp.start--;
            cur = parent;
            parent = HuffNode[cur].parent; // 往上一层
        }
        swap(HuffCode[i], tmp);
    }
}

int main() {
    cout << "Please input n:" << endl;
    cin >> n;
    HuffmanTree();
    HuffmanCode();
    for(int i = 0; i < n; i++) { // 输出所有的哈夫曼码
        cout << HuffNode[i].value << ": Huffman code is: ";
        for(int j = HuffCode[i].start + 1; j < n; j++) {
            cout << HuffCode[i].bit[j];
        }
        cout << endl;
    }
    return 0;
}

测试数据：

6
a 0.05
b 0.32
c 0.18
d 0.07
e 0.25
f 0.13

编码结果：

a: Huffman code is: 1000
b: Huffman code is: 11
c: Huffman code is: 00
d: Huffman code is: 1001
e: Huffman code is: 01
f: Huffman code is: 101

页面树结构

哈夫曼编码